Note: Tidal interactions, particularly the dissipation mechanisms described further down, were the focus of my PhD, undertaken at the University of Cambridge between 2011 and 2015.
If you’ve ever visited the sea shore, you’ll be aware of the tides. There’s usually a wide band of sand near the sea that is much wetter and firmer than the rest of the beach. If you stay for many hours you’ll notice the waterline advance inland until it’s covered up that wet sand, and then turn around retreat, uncovering more of the beach.
Most people know there are two high (and two low) tides a day, and that they have something to do with the Moon, and that’s about as far as they think about it. I spent a lot longer thinking about tides, because they turn out to occur in far more places than just the Earth. In some cases they may determine the fate of planets. But let’s stick with the Earth-Moon system for now, since it’s easy to picture.

In the figure above you can see the Earth and Moon. I’ve drawn a dashed circle for the shape the Earth would take if left to its own devices. The gravitational attraction from the moon acts just a little more strongly on the side of the Earth closest to the Moon and pulls up a tidal “bulge” on this side of the Earth. What is a little less intuitive is that there is also a bulge on the far side of the Earth. That side is further from the Moon than the rest of the Earth, and this lets mass sort of pile up there. I’ve massively exagerrated the bulge size in this picture - by a factor of roughly a million. The tide the moon raises on Earth actually has a height of a few meters.
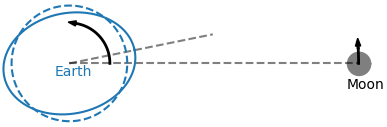
The tide gets a little more complicated when we consider the relative angular velocities of the Earth’s rotation and the Moon’s orbit. The Moon takes 28 times as long to complete one orbit as the Earth takes to complete a rotation. This results in the Earth’s tidal bulge being “dragged” ahead of the Moon by an angle called the tidal lag angle. The term lag is a bit misleading here, since the bulge is really leading ahead of the Moon, but it still gets used. It originates from the opposite scenario in which the planet is rotating more slowly than the moon is orbiting, in which case the bulge really does lag behind the moon. We’ll come back to this in the context of planets around other stars.
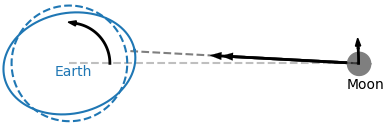
All that ocean raised up in the tidal bulge(s) has mass, and that mass creates a gravitational field that acts on the Moon. I’ve drawn the direction of this force in the figure just above. The bulge on the far side will also exert a force, but being further away it’s going to be smaller due to the \(1 / r^2\) law, so we’ll ignore it. The crucial thing to notice is that this force has a small component that is in the direction the Moon orbits in. It’s mostly pulling the Moon towards the Earth, but it’s very slightly pulling the Moon along the direction of its orbit too. It’s slightly accelerating the Moon. From orbital mechanics we know that this increases the radius of the orbit, and that’s a thing that has been measured by bouncing lasers off reflectors left on the Moon’s surface: the Moon is getting about 3.8cm further from the Earth each year.
Our First Bit of Math: Energy and Angular Momentum
Figuring out how the orbit of the Moon should change looks like it will involve predicting the lag angle of the Earth’s tidal bulge, and then computing an integral over the mass of the tidal bulge to figure out the gravitional effect on the Moon. It turns out we can actually bypass doing either of those things by looking at the energy and angular momentum.
There are three ways this system contains energy: the kinetic energy in the rotation of the Earth, the kinetic energy in the centre of mass motion of the Earth and Moon, and the gravitational potential energy of the Earth and Moon. The last two exchange energy back and forth if the orbit is non-circular, but there’s a simple formula for this total orbital (kinetic plus gravitational) energy that remains constant. We can write: \[ E = \frac{1}{2} I \Omega^2 - G \frac{M_E M_M}{2 a} \] Here \(I\) is the moment of inertia of the Earth, \(\Omega\) is the angular velocity of the Earth’s rotation, \(M_E\) and \(M_M\) are the mass of the Earth and Moon, \(G\) is the universal gravitational constant, and \(a\) is the semi-major axis of the Moon’s orbit. If you don’t know what a moment of interia is, you can think of it as a measure of how spread out the mass of a body is. It determines how resistant that body is to changing its rate of rotation, rather like how the mass of a body determines its resistance to changing its speed. For a circular orbit the semi-major axis, \(a\), is the same thing as the radius of the orbit.
The system also has angular momentum, contained in both the Earth’s rotation and the orbit: \[ L = I \Omega + \frac{M_E M_M}{M_E + M_M}a^2 n \] Here we’ve introduced a new symbol, \(n\). This denotes a quantity called the mean motion, which is the average angular speed of the orbit. For an elliptical orbit the angular speed is not constant (it’s greater when the bodies are closer to each other), but for circular orbits it is, and is equal to \(n\).
We now apply a bit of physics knowledge. The angular momentum of the system must be constant - angular momentum is convserved, and there is nowhere for it to go. But the energy can decrease, because energy can be dissipated to heat. This leads us to these two equtions: \[ \dot{a} = \frac{2(M_E + M_M)}{ M_E M_M } \frac{1}{n a} \frac{1}{(\Omega - n)} (-\dot{E}) \] \[ \dot{\Omega} = \frac{1}{I} \frac{1}{(n - \Omega)} (-\dot{E}) \]
Because energy can only be dissipated to heat, not vice versa, we must have \((-\dot{E}) > 0\). So every term on the right hand side of these equations is always positive, except possibly \((\Omega - n)\). In the case of the Earth-Moon system, the Earth rotates faster than the Moon: \(\Omega > n\). The two equations above then imply \(\dot{a} > 0\) and \(\dot{\Omega} < 0\). i.e. the Moon is getting further away, and the Earth’s rotation is slowing down.
Exoplanets and the Timescale of Fiery, Fiery Doom
I promised earlier that we’d talk about planets around other stars and a situation where the bulge really does lag behind the object raising it. A lot of the planets we know of orbiting stars other than the Sun (exoplanets) are very close to their star. The closer two bodies are to each other, the shorter the period of their orbit. In many cases these planets, called hot Jupiters, take only days to orbit their star. But stars take much longer to rotate - the Sun rotates every 27 days, for example. So these are systems with \(\Omega < n\), which tells us \(\dot{\Omega} > 0\) and \(\dot{a} < 0\).
The fact that \(\dot{\Omega} > 0\) is not particularly interesting. The moment of inertia, \(I\), of the star is so large that the rotation rate will not change very much. But the decrease in orbital radius, \(\dot{a} < 0\), is very interesting, because it presents a puzzle. If the dissipation rate, \((-\dot{E})\), were large, then the orbital radius would decrease rapidly. The planet would eventually be consumed and destroyed by the star. If these planets only survived for a few tens of thousands of years so close to their stars, it would be very surprising that were happened to see so many of them during such a brief period in their lifecycle - the timescale for fiery, fiery doom must be large. We can therefore be quite confident that \((-\dot{E})\) is not too high. But this still leaves the question of what determines the strength of this dissipation.
This is a partial write-up that so far has covered only the motivation for the problems I looked at in my thesis. I plan to expand this later and include description of the specific mechanisms I looked at, and what I found.